Langsung ke konten utama

Pembuktian Aturan Cosinus

Perlu diperhatikan, aturan sinus – cosinus dan luas segitiga diperoleh melalui sebuah garis tinggi (tegak) pada segitiga.
ATURAN COSINUS
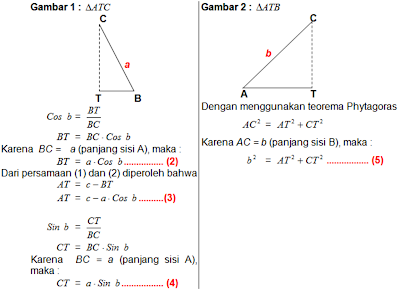
Perhatikan gambar berikut : (Garis tinggi melalui titik A)
AT merupakan garis tinggi yang melalui titik sudut A. Garis tinggi AT membagi segitiga ABC menjadi dua buah segitiga siku – siku yaitu segitiga ATB dan segitiga ATC.
BC = BT + CT
BT = BC – CT
Karena BC = a (panjang sisi a), maka :

















Dari persamaan (3), (4) dan (5) diperoleh bahwa :



















Perhatikan gambar berikut : (Garis tinggi melalui titik B)
BT merupakan garis tinggi yang melalui titik sudut B. Garis tinggi BT membagi segitiga ABC menjadi dua buah segitiga siku – siku yaitu segitiga ATB dan segitiga BTC.
AC = AT + CT
CT = AC - CT
Karena AC = b (panjang sisi b), maka : 
Dari persamaan (3), (4) dan (5) diperoleh bahwa :



















Perhatikan gambar berikut : (Garis tinggi melalui titik C)
CT merupakan garis tinggi yang melalui titik sudut C. Garis tinggi CT membagi segitiga ABC menjadi dua buah segitiga siku – siku yaitu segitiga ATC dan segitiga BTC.
AB = AT + BT
AT = AB - BT
Karena AB = c (panjang sisi c), maka : 















Dari persamaan (3), (4) dan (5) diperoleh bahwa :
Sehingga, dapat disimpulkan pada ATURAN COSINUS berlaku :
ATURAN COSINUS dapat digunakan apabila :
1. Diketahui 2 buah sisi dan 1 buah sudut yang diapit oleh kedua sisi tersebut.
2. Diketahui panjang ketiga sisinya.
Untuk mencari cosinus, sinus, dan tangen  TERBESAR, dapat dicari dengan aturan cosinus dengan memilih panjang sisi terbesar, dan sebaliknya.
Jika diketahui panjang ketiga sisi segitiganya, maka besar sudut a0, b0 dan c0 dapat ditentukan dengan rumus :
Klik disini : Modul Pembelajaran Aturan Cosinus
Download disini : Media Pembelajaran Aturan Cosinus
Lihat juga : Pembuktian Aturan Sinus

Label

Label:

Komentar

Posting Komentar

Postingan populer dari blog ini

Luas Segitiga Pada Trigonometri

1. JIKA DIKETAHUI 2 SISI DAN 1 SUDUT YANG DIAPIT OLEH KEDUA SISI Perhatikan ∆ATC : Sehingga diperoleh Luas Segitiga ABC sebagai berikut : Dengan demikian dapat disimpulkan jika diketahui dua buah sisi dan satu buah sudut yang diapit oleh kedua sisi tersebut pada segitiga sembarang, maka luas segitiganya adalah : 2.  JIKA DIKETAHUI 2 SUDUT DAN 1 SISI YANG MENGAPIT KEDUA SUDUT Dari persamaan (1) dan (2) diperoleh : Dengan cara yang sama (dengan menggunakan rumus Aturan Sinus), maka akan diperoleh : 3.  JIKA DIKETAHUI PANJANG KETIGA SISINYA Perhatikan ∆ABC adalah segitiga sembarang. Garis CT adalah garis tinggi yang ditarik dari titik C dan membagi ∆ABC menjadi 2 bagian, yaitu : ∆ATC dan ∆BTC. Pada  ∆ATC berlaku : Pada  ∆BTC  berlaku : Diketahui bahwa : s     =  ½ . keliling segitiga s     = ½ ( a + b + c ) 2 s    =  a + b + c sehingga diperole...
4 komentar
Baca selengkapnya

Bangun Ruang Sisi Datar

Bangun Ruang Sisi Datar adalah bangun ruang yang permukaan sisi - sisinya berbentuk datar. Beberapa contoh bangun ruang sisi datar antara lain : Kubus, Balok, Prisma dan Limas. Berikut ini merupakan modul pembelajaran bangun ruang sisi datar. Semoga bermanfaat. Lihat video pembelajarannya Kubus dan Balok disini :  Download disini : KUBUS DAN BALOK Lihat video pembelajarannya Prisma dan Limas disini : Download disini : PRISMA DAN LIMAS
Posting Komentar
Baca selengkapnya

PERSAMAAN TRIGONOMETRI

PERSAMAAN TRIGONOMETRI A. Persamaan Sinus Sin x 0 = Sin α 0 Untuk menentukan himpunan penyelesaiannya ada 2 cara, yaitu : 1.   x = α 0 + k . 360 0 2.   x = (180 – α) + k . 360 0 dimana : k є bilangan bulat ( k = 0, 1, 2, 3, … ) B. Persamaan Cosinus Cos x 0 = Cos α 0 Untuk menentukan himpunan penyelesaiannya ada 2 cara, yaitu : 1.   x = α 0 + k . 360 0 2.   x = (– α) + k . 360 0 dimana : k є bilangan bulat ( k = 0, 1, 2, 3, … ) C. Persamaan Tangen Tan x 0 = Tan α 0 Untuk menentukan himpunan penyelesaiannya ada 1 cara, yaitu : 1.   x = α 0 + k . 180 0 dimana : k є bilangan bulat ( k = 0, 1, 2, 3, … ) D. Persamaan a.sin x 0 + b.cos x 0 = c Kita ubah dulu a.sin x 0 + b.cos x 0 menjadi r. cos (x 0 – p 0 ) dimana : a = koefisien sin x 0 b = koefisien cos x 0 Download materinya disini : Persamaan Trigonometri Download soalnya disini :  Latihan Soal Persamaan Trigonometri ...
Posting Komentar
Baca selengkapnya